Exponential Growth? I have thoughts.

Ever since the start of what became known as the SARS-CoV2 Pandemic the word “exponential growth” has been all over the headlines. And it’s bad. Real scary.

“Just look at the curve, man! Pretty soon everyone will be…”, you know the drill.

After that exponential growth was used to justify military aid in Ukraine – “Stop the exponential aggression of Russia”, and recently the growing concerns about AI – “God Mode AI”.

Exponential graphs are scary because not only is there growth, but the speed of growth is constantly accelerating. The old fable of the king, the con-artist and the chess board is frequently mentioned to whip those in line who aren’t scared yet.

To recap: A king grants a con-artist a simple favor. The con-artist asks the king to take out a chessboard and put one grain of rice on the first square, two on the second, four on the third, and so forth. The king, calculus never being one of his strong suits, complies only to find out that all of his kingdom isn’t worth enough to buy that much rice.

BOOM! Told ya so! See, exponential growth is SCARY!

Well, it is! But it’s also exceedingly rare. It’s absolutely impossible in the world of physics, but can and does occur in mathematical worlds, and some of those have massive real-world impact.

What do I mean by that? Let’s stick to the example of the king and the chess board. Let’s say the king really commits to the con-artist and doesn’t just chop their head off for being insufferable smart asses after square number 8 or 9.

The table below shows how many grains of rice are in each field.

We’re still assuming the king is absolutely committed to fulfilling his offer, and time is no issue, because counting those damn grains is gonna take a loooong while.

We’re converting the grains to tons (yes 1000kg tons) of rice now, and assume each grain of rice weighs approx 0.05g on average, a number we got from the internet.

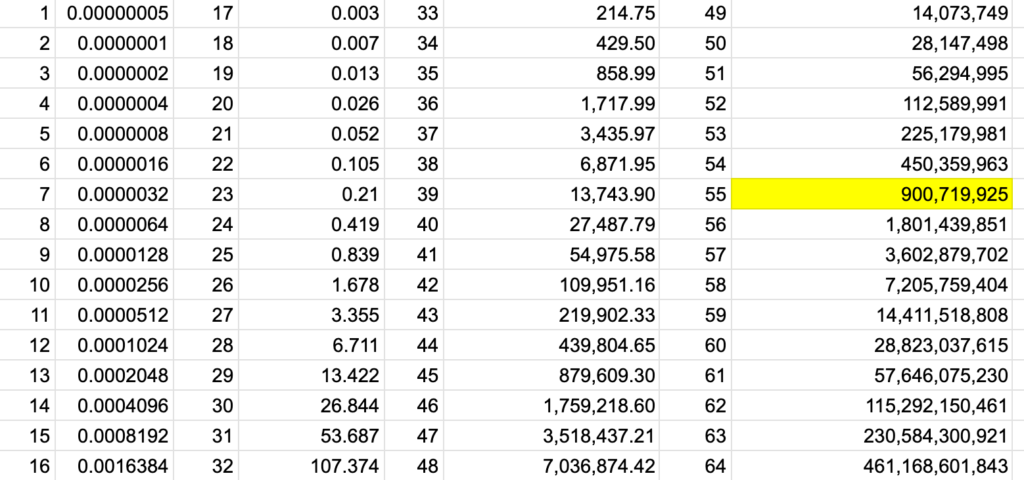
So at field 26 the king has to fork over a 1.68 tons of rice already. It starts to get expensive. But again, time is no issue, the logistics are all sorted. The wonders of modern agriculture managed to produce 756,743,722 metric tons of rice in 2022. As you can see at square #55 the poor king would already have to buy more than a full year of rice production worldwide. Ouch.

And here, I want to end the experiment. We can clearly see that the “exponential growth” would, even with the best of intentions, have likely ended somewhere around square #30, or at least slowed down considerably.

This dynamic is exactly what we always see in the natural world. Growth has limits! And that leads to an opposing force dampening growth acceleration at first and finally limiting it. The resulting function is called Sigmoid function, Gompertz Funktion in German.

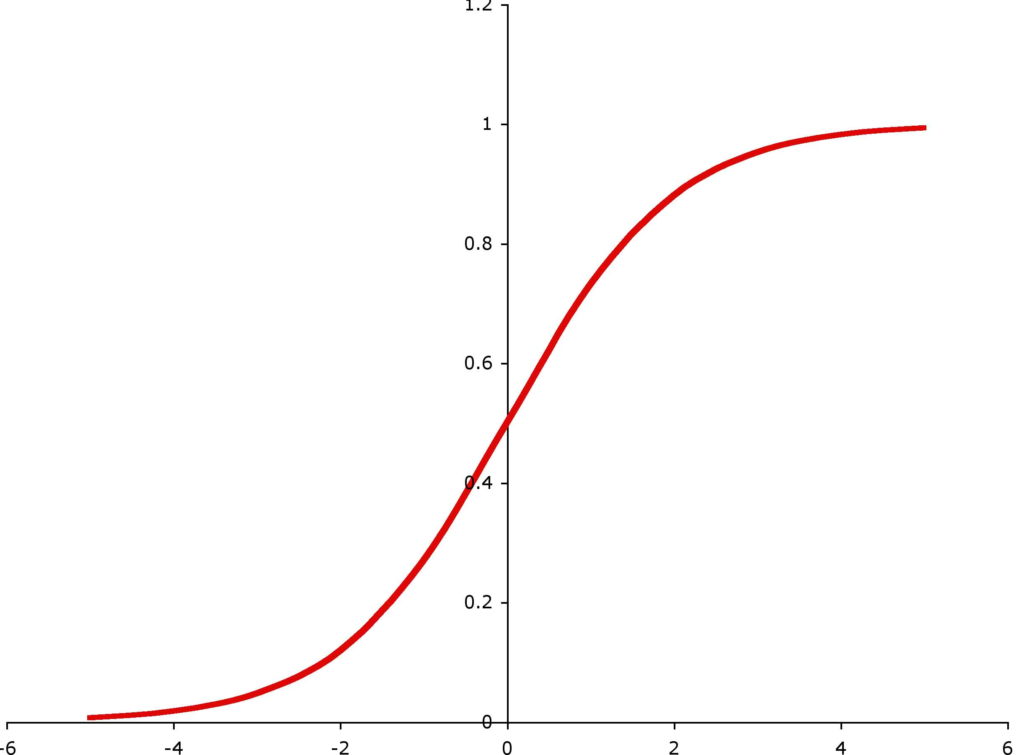
We can see the upper limit and we can see growth being somewhat close to exponential at the very beginning, then linear, and finally logarithmic before coming to a standstill.

Understanding the dynamics of the Sigmoid allows us to calibrate and predict with much higher accuracy then staying trapped in exponential scaremongering.

• Is growth still accelerating? -> okay, we’re right at the start of this.
• Is growth linear? -> Somewhere in the middle, we might be able to make some educated guesses about where the limit will be.
• Is growth already slowing down? -> Top signal.

We started out with a couple of popular scares. Let’s briefly look into them.

• Viral contagion -> Textbook sigmoid, the question becomes how many are susceptible to infection at all.
• Military aggression -> Sigmoid with a low threshold. There’s a clear limit to how many tanks and soldiers any nation can have.
• AI power -> Sigmoid. Processing capability is limited by chip supply. Neural nets have truly exponential costs of compute as they grow…

In my humble opinion, the poor exponential curve is the new scary ghost story. It mostly doesn’t exist if you shine a flashlight on it.

Where it does exist and has massive power is in finance. When growing a portfolio, the difference between a 2% and a 3% CAGR is massive over the years. Warren Buffet compared it to a snowball. The stickier the snow, the faster the growth.

Or inflation. In the 30s of the previous century, inflation in the Weimar republic grew exponentially. Even though in reality there was a soft dampening factor because it was a cash-only economy and the printing presses took some time. In the current cash-less economy, this could happen at a much quicker pace. Now that’s something to worry about as governments worldwide push trillions upon trillions of newly created money supply into the markets.

Don’t believe the hype, as Public Enemy shouted from the roof-tops.

And embrace the Sigmoid!